G検定の学習として、今回はディープラーニングを勉強していきます。まずは概要で、次の記事で手法を取り上げる予定です。
ディープラーニングの基本
ニューラルネットワークは、機械学習の手法の1つです。
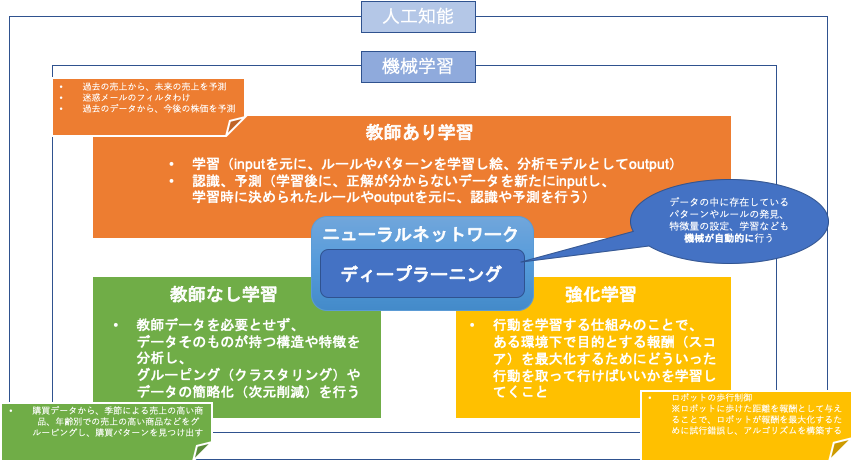
多層パーセプトロン
ニューラルネットワークは、あくまでも
入力と出力の関係性が、隠れ層の中に重みとして表現されているものです。

隠れ層は、
入力と出力を対応付ける関数に相当します。
もともとのニューラルネットワークの原点は、1958年のフランク・ローゼンブラットによる単純パーセプトロンでした。
これは単純なモデルで、隠れ層という概念がなく、線形分類しか行うことができないものでした。
そこを解消するために隠れ層を追加することで非線形分類ができるようになったものを多層パーセプトロンといいます。
ディープラーニング
ディープラーニングは、隠れ層を増やしたニューラルネットワークのことなので、多層パーセプトロンの要領で層を「深く」していくことで、ディープラーニング(深層学習)になります。

ただしこの説明は、ディープラーニングの基本形なので、
基本形以外の様々なモデルがあります。
あくまで、ディープラーニングはニューラルネットワークを応用した手法のため、ニューラルネットワークのモデル自体は、ディープニューラルネットワークと呼びます。
ニューラルネットワークの問題
隠れ層を増やしていけばディープラーニングにすることができ複雑な問題に対応することができると思うのですが、
ニューラルネットワークでは、
モデルの予測結果と実際の正解値との誤差をネットワークに逆向きにフィードバックさせる形でネットワークの重みを更新する誤差逆伝播法という方法をとります。
ここをさらにネットワークを深くすると、誤差が最後まで正しく反映されなくなってしまうという結果が得られてしまいました。

隠れ層を単純に増やすだけでは、
誤差逆伝播法で、誤差がフィードバックできなくなってしまうためモデルの精度が下がってしまうという事になっていました。。。
この問題の理由の1つが、シグモイド関数の特性によるものです。
(誤差はネットワークを逆向きに伝播していきますが、その過程で元々の誤差にいくつかの項をかけ合わされます。この項の1つに活性化関数の微分があり、こいつが問題でした。)
ニューラルネットワークの活性化関数として、シグモイド関数が使われていましたが、
これを微分した関数(導関数)が、こちら。
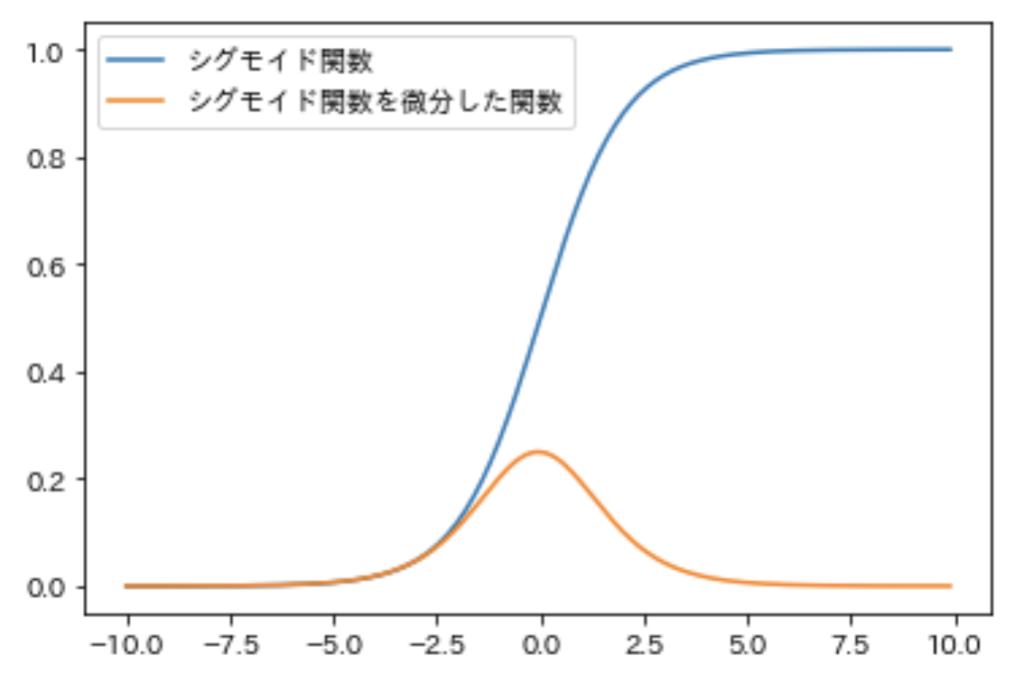
シグモイド関数の部分は最大値が0.25にしかならないのです。
つまり、1よりもかなり小さいので隠れ層を遡るごとに(活性化関数の微分が掛け合わされる)伝播していく誤差はどんどん小さくなっていくことになります。

つまり、
多くの隠れ層があると、
入力層付近の隠れ層に到達するまでには、もはやフィードバックすべき誤差がなくなってしまうことになるのです。
このことを、勾配消失問題といいます。
ディープラーニングの初期アプローチ
2006年に、毎度おなじみトロント大学のジェフリー・ヒントンがオートエンコーダー(Autoencoder)、自己符号化器という手法を提唱し、ディープラーニングは盛り上がりを取り戻しました。
オートエンコーダー
オートエンコーダーは、可視層と隠れ層の2層からなるネットワークのことです。
可視層とは、入力層と出力層がセットになったもののことを言います。
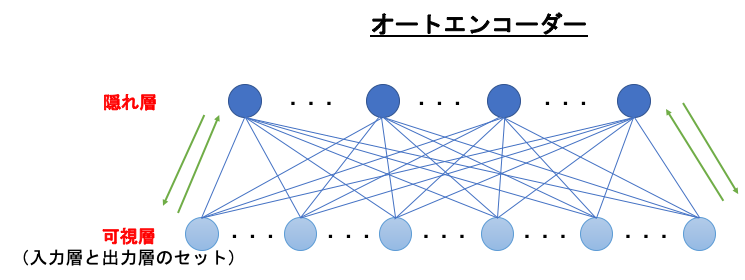
オートエンコーダーに与えられるinputは、
可視層(入力層) → 隠れ層 → 可視層(出力層)
の順に伝播し、outputされます。
ここから、オートエンコーダーは、inputとoutputが同じになるようなニューラルネットワークということになります。

inputとoutputが同じということは、
例えば手書きで「5」を書いた画像をinputしたら、
ネットワークが「5」を出力するように学習するということになりますね。
これによって、
隠れ層には、「入力の情報が圧縮されたもの」が反映されることになります。(入力層の次元から、隠れ層の次元まで情報が圧縮されることになります。)
→ 情報が要約されるようなイメージ

一度inputされた情報を要約して、それを元に戻すことでoutputとするので、
大事な情報だけが隠れ層に反映されていくということになります。
入力層 → 隠れ層 の処理を、エンコード(Endode)
隠れ層 → 出力層の処理を、デコード(Decode)
といいます。
積層オートエンコーダー
オートエンコーダーは、ディープニューラルネットワークではない(隠れ層が多層ではないため)のでここからどのように「ディープ」にすればいいのか?が考えられました。
結果、オートエンコーダーを積み重ねることでディープニューラルネットワークを構成する、ディープオートエンコーダーを作ること、
正確に言うと、
積層オートエンコーダー(Stacked Autoencoder)という手法が考えられました。
またまたあのトロント大学のジェフリー・ヒントンです。
積層オートエンコーダーのアプローチは、
オートエンコーダーを順番に学習させていき、それを積み重ねるというものでした。
従来だと一気にすべての層を学習するというものでしたが、入力層に近い層から順番に学習させるという、逐次的な方法をとっていきました。

例えば、オートエンコーダーAとオートエンコーダーBがあるとすると、
まずオートエンコーダーAが 可視層↔隠れ層の学習をそのまま行います。
これにより、オートエンコーダーAの重みが調整されます。
そして、オートエンコーダーAの隠れ層が、オートエンコーダーBの可視層になります。
次にオートエンコーダーBで学習が行われます。
こうしていくとどれだけ層が積み重なっても、順番に学習してくことでそれぞれの重みが調整されるので有効ということになります。
この、オートエンコーダーを順番に学習していく手順を、事前学習(Pre-Training)といいます。
ファインチューニング
オートエンコーダーを積み重ねるだけでは、どこまで行ってもラベルを出力することができないという落とし穴があります。
※ラベルは、データの印のことで、ラベルの情報はディープラーニングのモデルの学習とテストに使われるものです。
※こんな問題もあるようです。ディープラーニングの「教師ラベル不足」とNTTの解決策
オートエンコーダーのoutputはinputそのものなので、これ自体ではinputから適する情報だけをoutputする、教師なし学習の手法になるため、教師あり学習で使えないということになってしまいます。。。
そこで、
積層オートエンコーダーでは、オートエンコーダーを積み重ねて最後にロジスティック回帰層(シグモイド関数やソフトマックス関数による出力層)を足すことで、教師あり学習を実現しています。
※回帰問題では、ロジスティック回帰層ではなく、線形回帰層を足すことになります。(ロジスティック回帰は「回帰」と名前がついていますが分類問題に使うアルゴリズム)
この最後に足すロジスティック回帰層でも、重みの調整が必要になります。
事前学習 → ロジスティック回帰層を足す → ディープニューラルネットワーク全体で学習
こういう順番に学習が進んでいきます。事前学習で隠れ層の重みが調整されているので、ディープになっても誤差が適切に逆伝搬していくことになるのでOK。
この最後の仕上げのことを、ファインチューニング(Fine-Tuning)といいます。積層オートエンコーダーは、事前学習とファインチューニングの工程で構成されるということになります。
事前学習のある、教師あり学習になります。
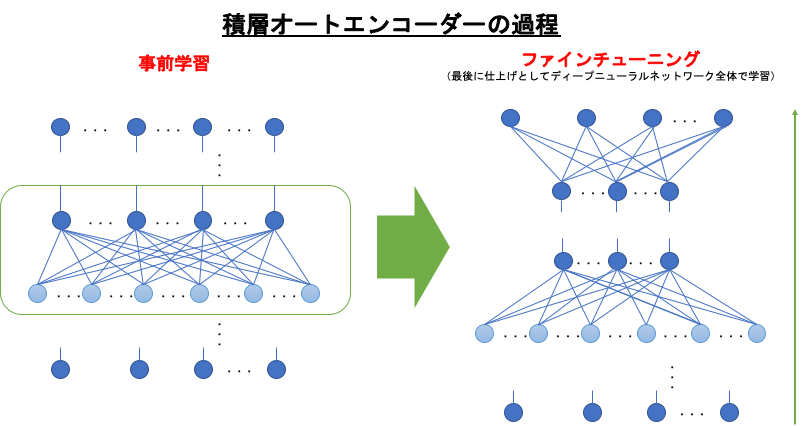
ちょっと分かりづらいので、別の説明も紹介します。
ファインチューニングとは、異なるデータセットで学習済みのモデルに関して一部を再利用して、新しいモデルを構築する手法です。モデルの構造とパラメータを活用し、特徴抽出器としての機能を果たします。手持ちのデータセットのサンプル数が少ないがために精度があまり出ない場合でも、ファインチューニングを使用すれば、性能が向上する場合があります。
キカガク

ここまでで、ディープニューラルネットワークが抱えていた「学習ができない」問題を、
事前学習というアプローチを入れることで解消できることができました!
深層信念ネットワーク
またまた登場、ジェフリー・ヒントンは2006年に深層信念ネットワーク(Deep Belief Networks)を手法も提唱しています。
教師なし学習(オートエンコーダーに相当する層)に制限付きボルツマンマシン(Restricted Boltzmann Machine)という手法を用います。

事前学習を用いた手法として、
- オートエンコーダーを使った、積層オートエンコーダー
- 制限付きボルツマンマシンを使った、深層信念ネットワーク
事前学習は今使われない
ここまで書いておきながら、最新手法では、
事前学習をしなくても一気にネットワーク全体を学習する方法(ディープラーニング)が考えられたため、事前学習は使われなくなりました。
層ごとに順番に学習をさせていくということは、計算コストが膨大になるというデメリットもあったためです。
ディープラーニングの実現方法
ディープラーニングのCPUとGPU
コンピュータには、CPU(Central Processing Unit)とGPU(Graphics Processing Unit)の2つの演算装置がありますが、
ディープラーニングの発展に大きく貢献しているのは、GPUの方です。
CPUは、様々な種類のタスクを順番に処理していくことが得意ですが、
GPUは、主に画像処理専用に演算を行うものです。大規模な並列演算処理に特化した存在としての位置づけでディープラーニングによく使われます。
こうした、画像処理以外の使用に最適化されたGPUを、GPGPU(General-Purpose Computing on GPU)といいます。
GPGPUのリーディングカンパニーは、カリフォルニア州サンタクララにある半導体メーカーNVIDIA社です。
なんと、ディープラーニング実装用のライブラリのほぼ全てがNDIVIA社製のGPU上での計算をサポートしています。
一方、Googleでは、テンソル計算処理に最適化された演算処理装置のTPU(Tensor Processing Unit)を開発しています。
テンサー・プロセッシング・ユニット(Tensor processing unit、TPU)はGoogleが開発した機械学習に特化した特定用途向け集積回路(ASIC)。グラフィック・プロセッシング・ユニット(GPU)と比較して、ワットあたりのIOPSをより高くするために、意図的に計算精度を犠牲に(8ビットの精度[1])した設計となっており、ラスタライズ/テクスチャマッピングのためのハードウェアを欠いている[2] 。チップはGoogleのテンサーフローフレームワーク専用に設計されているがGoogleはまだ他のタイプの機械学習にCPUとGPUを使用している[3] 。他のAIアクセラレータの設計も他のベンダーからも登場しており、組み込みやロボット市場をターゲットとしている。
Googleは同社独自のTPUは囲碁の人間対機械シリーズのAlphaGo対李世ドル戦で使用されたと述べた[2]。GoogleはTPUをGoogleストリートビューのテキスト処理に使っており、5日以内にストリートビューのデータベースの全てのテキストを見つけることができる。Googleフォトでは個々のTPUは1日に1億枚以上の写真を処理できる。TPUはGoogleが検索結果を提供するために使う「RankBrain」においても使用されている[4] 。TPUは2016年のGoogle I/Oで発表されたが、GoogleはTPUは自社のデータセンター内で1年以上前から使用されていると述べた[3][2]。
Googleの著名ハードウェアエンジニアのNorm Jouppiによると、TPU ASICはヒートシンクが備え付けられており、データセンターのラック内のハードドライブスロットに収まるとされている[3][5]。2017年時点でTPUはGPUTesla K80やCPUXeon E5-2699 v3よりも15~30倍高速で、30~80倍エネルギー効率が高い[6][7]。
Wikipedia
GoogleのTPUって結局どんなもの? 日本法人が分かりやすく説明
ディープラーニングで必要なデータ量の目処
ディープラーニングは、機械学習の1つなのでデータを元に学習をしていきますが、
その学習とは、モデルが持つパラメータの最適化になります。
ディープニューラルネットワークはネットワークが深くなればなるほど最適化するべきパラメータ数も増えてきて計算も多くなります。
そこで問題が、
一体どれだけのデータが必要なの???
ということです。
その答えとしては、
決まった数字は無い。
となります。

とはいえ、データ量の目安となる経験則は存在しています。
バーニーおじさんのルールという経験則では、
モデルのパラメータ数の10倍のデータ数が必要
となっています。
その他
これよくまとまっていて、ここまでの記事を見たあとにさらっと見ると良さげ。
参考資料
深層学習教科書 ディープラーニング G検定(ジェネラリスト) 公式テキスト (日本語) 単行本(ソフトカバー)
徹底攻略 ディープラーニングG検定 ジェネラリスト 問題集 徹底攻略シリーズ Kindle版





